Un plasma entre deux grains de raisin au four microonde
Voici tout d’abord une expérience que l’on peut facilement effectuer si l’on dispose d’un four microonde et d’un grain de raisin :
» Couper le grain en deux hémisphères; les placer côte à côte sur un verre de montre ou une plaquette de verre dans le microonde et mettre celui-ci en route pour quelques secondes.
Vous allez observer presque instantanément par la vitre du four une étincelle et voir jaillir un arc électrique au point de contact des demi-grains. »
Si vous n’avez pas pu faire l’expérience, regardez la vidéo suivante.
Vidéo du plasma obtenu par irradiation dans un four microonde ordinaire de deux demi-grains de raisins placés côte à côte dans un verre de montre :
Tiré de Linking plasma formation in grapes to microwave resonances of aqueous dimers
Hamza K. Khattak, Pablo Bianucci, and Aaron D. Slepkov, PNAS, 2019 (CC BY-N
Ces arcs, qui correspondent à une ionisation de l’air sous l’action d’un champ électrique et qui forment un plasma, ont suscité depuis deux décades de nombreuses explications dont aucune n’était satisfaisante.
Des scientifiques de la Trent University, Peterborough et de la Concordia University, Montreal, toutes deux au Canada, ont trouvé, en s’appuyant sur quelques expériences simples, un modèle physique expliquant entièrement ce phénomène
La première explication qui en avait été donnée était que les deux grains formaient une antenne dipolaire dans le champ microonde et qu’un courant passait par un point de forte conductivité entre les deux grains, créant un plasma. Dans le cas des demi-grains cela pouvait se comprendre, l’endroit du contact des peaux de raisin mouillées remplit le critère de plus forte conductivité. Mais dans le cas des grains de raisin entiers (voir la vidéo ci-dessous), leur surface est sèche et le phénomène existe néanmoins..
Vidéo du plasma créé par irradiation dans un four microonde de cuisine de deux grains de raisins entiers placés sur un verre de montre :
Vidéo tirée de Linking plasma formation in grapes to microwave resonances of
aqueous dimmers, Hamza K. Khattak, Pablo Bianucci, and Aaron D. Slepkov, PNAS, 2019 (CC BY-NC-ND).
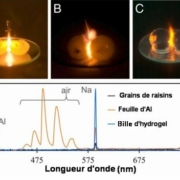
La figure 1 ci-dessous montre des photos de l’expérience réalisée avec deux hémisphères de raisin, deux grains de raisin entiers et deux billes d’hydrogel (>99% d’eau et aucune peau) et les spectres d’émission optique dus à ces trois expériences
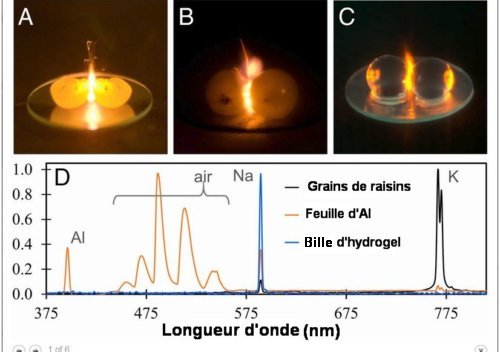
Fig.1. Plasma créé dans 3 géométries différentes
A) Plasma entre deux hémisphères de raisin reliés par un lambeau de peau (arrangement traditionnel).
B) Plasma entre deux grains entiers de raisin.
C) Plasma entre deux sphères d’hydrogel (<99 % d’eau, pas de peau).
D)Spectres d’émission pris à travers la vitre du four microondes. ICela montre que le plasma est induit dans les raisins par le potassium K et par le sodium Na dans les billes d’hydrogel trempées dans une solution de sel ordinaire (NaCl).
Tiré de Linking plasma formation in grapes to microwave resonances of
aqueous dimmers, Hamza K. Khattak, Pablo Bianucci, and Aaron D. Slepkov, PNAS, 2019. (CC BY-NC-ND).
La vidéo suivante montre le cas (C ci-dessus) des 2 sphères d’hydrogel :
Vidéo du plasma créé par irradiation dans un four microonde de cuisine de deux sphères d’hydrogel :
Vidéo tirée de Linking plasma formation in grapes to microwave resonances of
aqueous dimmers, Hamza K. Khattak, Pablo Bianucci, and Aaron D. Slepkov, PNAS, 2019 (CC BY-NC-ND).
La formation du plasma à partir de deux sphères aqueuses
Les chercheurs ont déduit de ce qui précède que l’exigence d’un pont de peau était superfétatoire, il ne servait qu’à établir entre les deux parties un contact qui sans cela est réalisé par l’appui des deux hémisphères l’un contre l’autre. Ils ont utilisé par la suite un verre de montre où les sphères sont maintenues délicatement au contact par leur propre poids.
Le spectre d’émission optique du plasma suggère que le potassium et le sodium, abondants dans la peau des raisins, sont ionisés par une concentration de champ électrique près du point de contact.
Les ions peuvent être mis en résonance par le rayonnement microonde bien que la longueur d’onde dans l’air de la radiation de fréquence 2,45 GHz des fours microonde (~12 cm) soit plus grande que la taille des grains (~1,5 à 2 cm). Car, à cette fréquence, la constante diélectrique de l’eau valant 80 fois celle de l’air, l’onde est ralentie, sa longueur d’onde dans l’eau est environ 9 fois plus petite que dans l’air et donc inférieure à la taille des grains.
La meilleure façon d’établir que ce sont des résonances, dites de Mie, qui créent le point chaud entre les deux sphères serait de mesurer la distribution du champ électrique à l’intérieur des sphères diélectriques et tout près de leur surface. Mais c’est extrêmement difficile. Or l’eau absorbe les ondes microondes ce qui la chauffe (d’où le four microonde !). Avec une caméra thermique (à infrarouge) on peut avoir une mesure indirecte de l’intensité du champ intégrée sur le temps de la mesure. Il faut noter que la carte thermique représente des températures de surface et non celles internes. Pour obtenir l’image de la température du centre des sphères, il faudra les couper en deux après ou avant l’exposition aux microondes.
La figure 2 ci-après montre des images de la caméra thermique qui sont de véritables cartes de la répartition des températures. On a utilisé ici des objets un peu plus grands que précédemment pour avoir un vue plus précise de la répartition du champ électrique moyen.
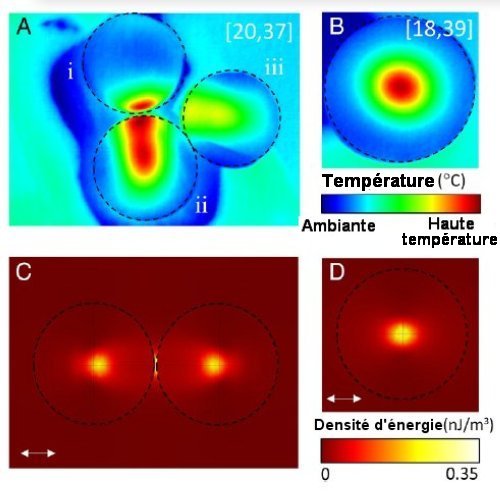
Fig.2. Cartes thermiques de billes d’hydrogel de 5,5 cm de diamètre
A) Distribution de la température après une irradiation de 4 secondes au four microonde d’un groupe de 2 billes accolées. On y voit bien l’importance d’obtenir une image à partir du plan de section qui intéresse l’opérateur. La bille i est une sphère complète, on y voit seulement un point chaud à sa surface près du point de contact ; les régions ii et iii sont des sphères sœurs de celle en i, mais elles ont été coupées en deux et leurs sections placées horizontales. On a pu ainsi montrer la distribution thermique sur le plan équatorial des hémisphères ii et iii .
B) On voit là la distribution de température après irradiation d’une sphère identique à la bille i mais coupée en deux : c’est un mode confiné radial qui a un maximum de température en son centre. Les températures minimale (ambiante) et maximale (haute température) sont indiquées en A) et B)
C) et D) Simulations de la densité d’énergie électromagnétique des géométries A) et B) pour des billes de 55 mm de diamètre et une séparation de deux des billes de 1 mm. Les flèches indiquent la direction de la polarisation du champ électrique. Notez le point chaud entre les deux billes dans C), il correspond à un point de fort champ électrique.
Tiré de Linking plasma formation in grapes to microwave resonances of
aqueous dimmers, Hamza K. Khattak, Pablo Bianucci, and Aaron D. Slepkov, PNAS, 2019 (CC BY-NC-ND).
Les chercheurs canadiens ont réalisé des simulations (Fig.2.C et D) du champ électrique dans les billes d’hydrogel en utilisant leur modèle théorique basé sur les résonances de Mie.
Le bon accord entre théorie et expérience obtenu par une combinaison de vidéos, de simulations numériques et d’imagerie thermique infrarouge montre que la formation de plasma avec des grains de raisins dans un four microonde s’explique par des résonances à ces fréquences microondes dépendantes de la forme des objets, qu’on appelle aussi résonances de Mie. Les grains de raisins agissent comme des sphères d’eau et, grâce à leur fort indice de réfraction et à leur faible coefficient d’absorption constituent, à 2,4 GHz, des résonateurs de qualité moyenne. Les résonances de Mie dans les sphères isolées s’ajoutent quand elles sont rapprochées, créant au point de contact un champ intense suffisant pour ioniser les atomes de sodium et de potassium, ce qui forme un plasma.
Comme l’eau a un plus grand indice de réfraction à 2,4 GHz que tout diélectrique connu aux fréquences du visible, on peut ainsi explorer des résonances géométrique en régime microonde, qui seraient inaccessibles dans le domaine visible.
Ce travail fournit des opportunités expérimentales pour modéliser les phénomènes de résonance à échelle nanophotonique en utilisant des objets homothétiques à échelle plus élevée irradiés en microonde ou encore aider à réaliser un type récent de laser, le spaser où, dans une structure nanoscopique, les photons sont remplacés par des oscillations de plasma de surface.
Nous voici bien loin de l’expérience de physique amusante dans notre cuisine !
Pour en savoir plus :
Linking plasma formation in grapes to microwave resonances of aqueous dimmers,
Hamza K. Khattak, Pablo Bianucci, and Aaron D. Slepkov, PNAS, 2019