Quand explosent les ballons de baudruche
La façon dont un corps se casse et se fragmente a toujours intéressé physiciens et ingénieurs car elle concerne de nombreux processus industriels et phénomènes géophysiques. Deux physiciens du Laboratoire de Physique Statistique de l’ENS à Paris ont étudié expérimentalement le processus de fragmentation de membranes de baudruche. Grâce à une caméra rapide, ils ont pu suivre dans le temps et l’espace l’évolution de cette fragmentation particulière qui devrait aider à comprendre les diverses figures de fracture observées dans les matériaux cassants.
Quand on perce un ballon de baudruche modérément gonflé, un accroc le parcourt, le découpant en quelques morceaux aux contours droits ou sinueux. Au contraire, un ballon fortement gonflé éclate en nombreux fragments. C’est ce qu’illustre la figure suivante.
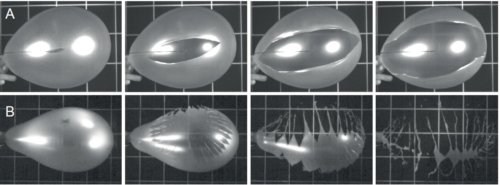
Fig.1. Les deux régimes d’explosion d’un ballon de baudruche.
A- Eclatement d’un ballon peu gonflé.
B- Eclatement d’un ballon fortement gonflé.
L’intervalle de temps entre deux images successives est de 0,3 ms. Chaque carré de la grille a un côté de 10 cm.
Crédit Sébastien Moulinet and Mokhtar Adda-Bedia, PRL 115, 184301 (2015).
Pour essayer de comprendre la transition entre ces deux régimes d’explosion, S. Moulinet et M. Adda-Bedia ont imaginé un dispositif expérimental d’observation et de mesure de la fragmentation. Une feuille de latex est pressée dans un cadre muni d’une ouverture circulaire de 52 mm de diamètre. De l’air comprimé permet de gonfler la feuille en obtenant un ballon axisymétrique jusqu’à ce qu’il heurte la pointe d’une lame de cutter. La pression à l’intérieur du ballon est mesurée et enregistrée. La mesure de la pression et l’image latérale obtenue par la caméra 2 permettent de connaître la force T normale à la section de la membrane au pôle du ballon. T représente la tension de la membrane.
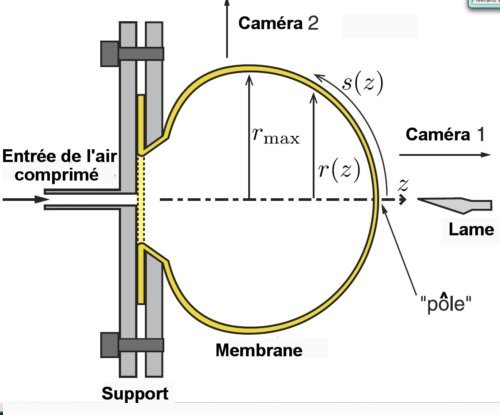
Fig.2 Schéma de l’appareillage utilisé pour l’étude de la fragmentation.
La membrane en latex est tenue entre les deux flasques du support à gauche.
La lame à droite peut être déplacée à volonté par rapport à la membrane ou rester fixe pendant que celle-ci grossit. On peut ainsi opérer en gonflant la membrane jusqu’au contact de la lame fixe ou déplacer celle-ci jusqu’au contact de la membrane gonflée à un volume donné.
Adapté avec autorisation de Sébastien Moulinet and Mokhtar Adda-Bedia, PRL 115, 184301 (2015). © APS.
Quand on injecte l’air comprimé, la feuille de latex se gonfle, prenant la forme d’un ballon asymétrique mais présentant une symétrie autour de l’axe z de la figure 2. Et cela jusqu’à ce que le pôle du ballon touche le bout de la lame placée en un point fixe de l’axe, ce qui entraîne son explosion. Une caméra rapide (caméra 1 Fig.2.) placée devant le dispositif enregistre l’explosion à une vitesse allant de 30 000 à 60 000 images/s. Une deuxième caméra ordinaire (25 images/s) prend une vue latérale du ballon. Selon la position plus ou moins éloignée du cadre de la lame, l’explosion se produit à une pression plus ou moins forte.
On observe un premier régime dit d’ouverture, à faible pression (Fig.3. A) : dès que la membrane touche la lame, un trou se forme qui crée un ou deux fentes qui découpent l’échantillon en peu de morceaux.
Le second régime (Fig.3. B) est celui dit de fragmentation. Il survient à plus forte pression par explosion spontanée ou induite par la lame placée à bonne distance de la membrane. De nombreuses déchirures rayonnent à partir du point de rupture initial.
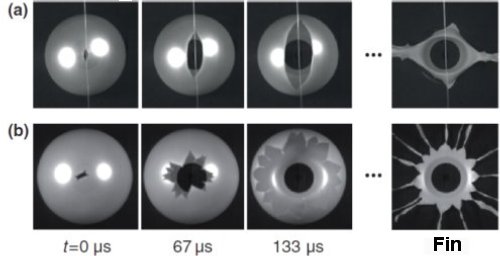
Fig.3. Images obtenues à la caméra rapide des deux régimes d’explosion observés.
A- Régime d’ouverture. Une fracture simple découpe en deux la membrane.La ligne verticale sur les images est celle du support de la lame ;
B- Régime de fragmentation.
Crédit Sébastien Moulinet and Mokhtar Adda-Bedia, PRL 115, 184301 (2015). © APS.
Les mesures effectuées ont permis de montrer que, pour une épaisseur donnée e de la membrane, il existe une valeur seuil de la force T qui sépare les deux régimes.
Dans le régime d’ouverture, les mesures à la caméra rapide ont montré qu’une déchirure progressait à une vitesse constante. Celle-ci augmente avec la force Tr appliquée au moment de la rupture.
Au contraire, dans le régime de fragmentation, la vitesse de progression des déchirures est indépendante de la force Tr. Ceci définit une vitesse limite de fragmentation atteinte au seuil de transition entre les deux régimes ; elle a pour valeur 570 m/s.
La vidéo suivante présente les deux régimes d’explosion d’un ballon, puis les différents aspects de l’expérience avec le montage de la figure 2 :
[jwplayer mediaid= »20865″]
Crédit Sébastien Moulinet.
On a déjà observé des fragmentations analogues à celles des membranes de latex dans des matériaux cassants soumis à des chocs. L’instabilité dynamique que traduit la transition entre deux régimes est commune à ces différents systèmes. La prédiction de la distribution des différentes tailles de fragments nécessite des modèles théoriques qui prennent en compte cette instabilité. Les résultats des expériences précédentes vont pouvoir servir à la construction et à la vérification de ces modèles.
Pour en savoir plus :
Popping Balloons: A Case Study of Dynamical Fragmentation
Sébastien Moulinet and Mokhtar Adda-Bedia
PHYSICAL REVIEW LETTERS 115, 184301 (2015)