Dans de nombreuses opérations industrielles, il est fréquent d’avoir à déposer à grande vitesse des quantités précises de fluides viscoélastiques. On peut citer le collage de composants électroniques, l’agroalimentaire et la fabrication de pièces par impression 3D.
Les liquides visqueux ordinaires, dits Newtoniens, par exemple les huiles, sont caractérisés par un rapport constant entre la contrainte exercée sur elles et le taux de cisaillement qu’elles présentent. La viscosité d’une substance caractérise sa capacité à dissiper de l’énergie.
Les matériaux élastiques se déforment sous la contrainte et retournent à leur état d’origine, montrant ainsi une capacité à acquérir de l’énergie et à la restituer.
Les polymères sont tous viscoélastiques mais aussi de nombreux autres corps.
Une équipe internationale de chercheurs (Graduate University, Okinawa, Japon, Eindhoven University of Technology, Eindhoven, Pays Bas et Northwestern University, Evanston, Illinois, Etats- Unis) a mis au point une nouvelle technique pour le dosage précis de ces produits.
La méthode de rupture nette par torsion
La figure suivante représente un processus typique de dosage d’un produit fluide. Au début de celui-ci, un pont liquide cylindrique relie la buse d’injection au substrat. Le recul de la buse au-dessus d’une hauteur critique Hc entraîne une déstabilisation du pont et un amincissement sous l’effet de la tension superficielle du liquide. Si ce dernier est viscoélastique, le retrait de la buse crée des gouttes satellites et une longue queue capillaire qui peut contaminer le substrat. En appliquant une torsion à un pont liquide viscoélastique, on fait se propager une indentation latérale vers le centre du pont entraînant une rupture du pont à une hauteur bien inférieure à Hc, ce qui évite gouttes satellites et queue capillaire.
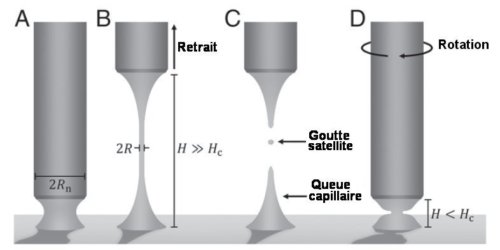
Fig.1. Un processus de dosage
A) Un pont liquide cylindrique de hauteur H connecte la buse de rayon Rn au substrat.
B) Le retrait de la buse à une hauteur H bien supérieure à une hauteur critique Hc déstabilise le pont et entraîne son amincissement sous l’effet de la tension superficielle.
C) Pour les ponts liquides viscoélastiques, le retrait de la buse crée des gouttelettes satellites et une longue queue capillaire qui peuvent contaminer le substrat. D) En appliquant une torsion à un pont liquide viscoélastique une indentation se propage vers le centre du pont, entraînant une rupture même à H < Hc. Tiré de Torsional fracture of viscoelastic liquid bridges San To Chana, Frank P. A. van Berlob, Hammad A. Faizic, Atsushi Matsumotoa, Simon J. Hawarda , Patrick D. Andersonb, , and Amy Q. Shena, PNAS 2021 Vol. 118 No. 24 Licence CC BY-NC-ND 4.0.
Dans le cas des ponts liquides viscoélastiques, le retrait de la buse crée des gouttes satellites et une longue queue capillaire. Tout ceci peut contaminer le substrat.
L’application d’une torsion à un pont liquide viscoélastique stable propage une indentation vers l’axe du pont, ce qui le coupe à une hauteur H < Hc.
La stabilité du pont dépend de la gravité, de la tension superficielle et de ses paramètres géométriques. On peut calculer la hauteur critique Hc à partir de ces facteurs.
L’appareillage utilisé pour étudier l’évolution de ces ponts consiste en 2 plaques circulaires concentriques : la plaque inférieure peut être déplacée selon un axe vertical, la plaque supérieure peut être mise en rotation.
On peut injecter entre les plaques un liquide occupant l’intervalle.
En utilisant des caméras rapides et en réalisant des simulations, les chercheurs ont pu montrer qu’une torsion peut couper un pont liquide capillaire stable en un temps de l’ordre de 1 s.
La figure ci-dessous illustre ce comportement pour un liquide viscoélastique.
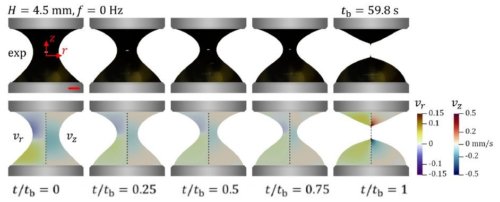
Fig.2 Expérience et simulation de la dynamique de rupture d’un pont liquide viscoélastique.
Un pont liquide de hauteur H= 2,5 mm se rompt sous l’effet d’une rotation de fréquence 35,3. Hz.
Ligne du haut. Combinaison d’images expérimentales et du champ de vitesse de pont liquide calculé par simulation.
Ligne du bas. Simulation des champs de vitesse radial et axial.
Tiré de Torsional fracture of viscoelastic liquid bridges San To Chana,1 , Frank P. A. van Berlob, Hammad A. Faizic, Atsushi Matsumotoa, Simon J. Hawarda , Patrick D. Andersonb, , and Amy Q. Shena, PNAS 2021 Vol. 118 No. 24 Licence CC BY-NC-ND 4.0.
La vidéo suivante correspond à l’expérience de la fig.2.
Vidéo d’un pont de liquide viscoélastique
Tiré de Torsional fracture of viscoelastic liquid bridges San To Chana,1 , Frank P. A. van Berlob, Hammad A. Faizic, Atsushi Matsumotoa, Simon J. Hawarda , Patrick D. Andersonb, , and Amy Q. Shena, PNAS 2021 Vol. 118 No. 24 Supporting information Licence CC BY-NC-ND
Sous une faible distance entre les deux plaques comme ici, H = 2.5 mm, le pont liquide est stable et l’action conjuguée de la tension superficielle et de la gravité ne suffisent pas à le rompre sans une rotation d’une des plaques. Une fois la rotation appliquée, la partie supérieure du pont est comme un solide en rotation tandis que la partie inférieure est plutôt stationnaire. Ceci localise la contrainte autour du col du pont liquide.
Les simulations réalisées reproduisent fidèlement les résultats expérimentaux tant pour les fluides viscoélastiques que pour les fluides Newtoniens. Les modèles utilisés permettent donc de pouvoir établir des protocoles pour le dépôt ou l’injection de fluides adaptés aux différents besoins de l’industrie alimentaire, de l’industrie électronique et de l’impression 3D.
Pour en savoir plus :
Torsional fracture of viscoelastic liquid bridges
San To Chana,1 , Frank P. A. van Berlob, Hammad A. Faizic, Atsushi Matsumotoa, Simon J. Hawarda , Patrick D. Andersonb, , and Amy Q. Shena, PNAS 2021 Vol. 118 No. 24 Licence CC BY-NC-ND 4.0


