Des surfaces transformables qui diminuent la résistance de l’air
Modifier les caractéristiques d’une surface peut changer les fonctionnalités de celle-ci. Les requins peuvent, en modifiant la structure de leur peau, diminuer la force de friction avec l’eau, responsable de la résistance à l’avancement qu’on appelle la traînée. On a constaté depuis longtemps que les empreintes en creux des balles de golf augmentent leur portée. Des chercheurs du MIT ont imaginé des surfaces courbes « intelligentes » capables de se plisser et ainsi de modifier à la demande leur topographie et ils ont pu en mesurer les conséquences aérodynamiques.
En effet, la rugosité particulière d’un corps solide autour duquel s’écoule un fluide peut abaisser la vitesse à laquelle se produit la transition laminaire-turbulente de l’écoulement. Ceci entraîne une diminution de la trainée.
A une certaine vitesse (d’autant plus élevée que la viscosité l’est et que la longueur caractéristique du solide est petite), l’écoulement devient turbulent avec l’apparition de tourbillons de vitesse, désordonnés et difficilement prévisibles.
La turbulence diminue à son début la traînée aux alentours de cette transition laminaire -turbulent. Cet effet est exploité pour des combinaisons de nageurs, les balles de golf et même à la surface d’ailes d’avions. Mais, si la vitesse augmente bien au delà de celle de la transition, la force de traînée réaugmente.
L’obtention de surfaces courbes transformables
Pour réaliser des surfaces transformables à volonté, les chercheurs ont fabriqué des sphères dotées d’une coque extérieure mince et rigide adhérant à une coquille faite d’un matériau mou dix fois moins rigide. Cette coquille intérieure est munie d’une cavité sphérique de rayon R0 (Fig.1 A). La diminution de la pression de l’air à l’intérieur de la cavité entraîne un plissage progressif de la surface extérieure, plissage que l’on peut ainsi contrôler. La fabrication se fait par moulage d’hémisphères collés entre eux pour obtenir des sphères.
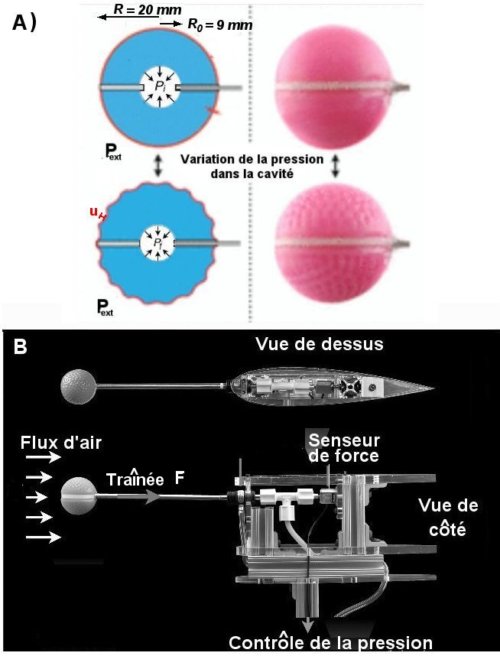
Fig.1. Schéma des sphères et photographie du dispositif de mesure de la traînée en soufflerie.
A) Schéma de la déformation de surface des sphères sous l’effet de la variation de pression. Une sphère (en haut), de surface lisse, devient ridée (en bas) quand on abaisse la pression de sa cavité. Ces sphères de 20 mm de rayon R sont obtenues par collage de deux hémisphères faits d’une coque fine (0,5 mm) de matière rigide entourant une coque de matière molle 10 fois moins rigide.
B) La sphère est montée sur un tube communiquant avec sa cavité. Ce tube coulisse sans frottement sur un support qui mesure la force exercée sur la sphère par le flux d’air. Un tuyau permet de pomper l’air contenu dans la cavité de la sphère. Crédit Advanced Materials, D. Terwagne et al..
Le profil de la surface de la sphère est analysé dans la soufflerie même par imagerie numérique et, pour une précision maximale, par balayage laser à 3 dimensions.
La vidéo suivante montre la déformation de la surface obtenue par ce procédé : l’expérience est réalisée sur une hémisphère.
[jwplayer mediaid= »19516″]
Crédit D.Terwagne, P. M. Reis
On peut donc mesurer la traînée tout en faisant varier le profil de surface de la sphère.
Les résultats des mesures
On a l’habitude de caractériser la résistance à l’avancement d’un corps solide dans un fluide par le coefficient de traînée Cx.
Les mesures du coefficient de traînée en fonction de l’état de surface ont été faites avec des sphères échantillons dont le relief obtenu par forte dépression ressemblait aux petits creux d’une balle de golf.
Avec une sphère lisse, on observe dans la soufflerie un Cx approximativement constant ( Cx≈ 0,5) en fonction de la vitesse dans le régime laminaire. En diminuant la pression à l’intérieur de la cavité de la sphère, sa surface s’orne de creux similaires à ceux d’une balle de golf, la transition laminaire-turbulent s’établit sans qu’on modifie la vitesse. Pour une diminution de pression de 380 mbars , la rugosité de surface est telle qu’ on obtient un Cx près de deux fois moins élevé. En diminuant la pression, on peut augmenter progressivement la profondeur des creux de la sphère ; on observe bien alors que la transition laminaire-turbulent se produit pour des valeurs plus faibles de la vitesse. Avec des sphères lisses ou ayant des reliefs moins profonds en forme de labyrinthe, on obtient au contraire une augmentation du Cx, donc de la traînée, après la transition laminaire-turbulent.
Ces résultats expliquent bien que, pour une même impulsion de départ, les balles de golf à empreintes en creux, soumises à une traînée moins élevée que les balles lisses, atteignent des plus grandes distances que celles-ci.
Une retombée théorique
Cette étude de l’aérodynamisme des sphères a conduit les chercheurs à s’interroger sur le processus par lequel s’était déformée la surface des sphères constituées d’une couche fine rigide sur substrat mou. Ils ont donc conçu un modèle théorique général de la surface courbe d’un système formé d’une couche fine rigide sur un substrat mou. Il est basé sur un analyse fine de la rupture de symétrie qui se produit au moment de la modification de courbure et est en parfait accord avec l’expérience.
En témoigne la figure suivante où l’on voit, en haut, des plissages de la surface de la sphère ainsi calculés et, en bas, des plissages correspondants expérimentalement observés par la méthode précédente. Sur la première colonne, on reconnaît le motif « balle de golf ». A pression interne plus élevée (deux colonnes de droite), le profil de surface tend vers des figures moins profondes et d’aspect labyrinthique.

Fig. 2. Plissages de sphères à couche de surface fines et rigides sur substrat mou.
a, b et c : Images de reliefs obtenus par calcul à partir du modèle.
d,e et f : Reliefs correspondants obtenus expérimentalement sur des sphères échantillon. Le paramètre adopté ici est le rapport du rayon R de la sphère à l’épaisseur constante h du film. Plus la pression est faible dans la cavité, plus R diminue et donc R/h également.
Sur les images calculées, u (voir Fig.1A) représente en couleurs la profondeur des motifs. La couleur rouge indique des points à l’intérieur de la sphère, la couleur bleue des points à sa périphérie.
Adapté avec permission de Norbert Stoop, Romain Lagrange, Denis Terwagne, Pedro M. Reis, and Jörn Dunkel NATURE MATERIALS | VOL 14 | MARCH 2015 |
© 2015 NPG.
Cette approche théorique peut servir à la prédiction des modifications des surfaces aérodynamiques précédentes mais présente aussi un intérêt en biologie pour la prédiction et le contrôle des processus de plissements de tissus vivants et la morphogenèse du développement embryonnaire.
Les surfaces transformables de façon continue et précise devraient pouvoir trouver des applications dans de nombreuses structures aérodynamiques. Pouvoir modifier une topographie de surface rapidement par variation de pression est extrêmement intéressant. La vitesse de réaction d’un tel système n’est limitée que par la vitesse du pompage qu’on peut utiliser. La réduction de la traînée aérodynamique présente pour les industries automobiles et aéronautique un inestimable intérêt.
Pour en savoir plus :
Smart Morphable Surfaces for Aerodynamic Drag Control
Denis Terwagne , Miha Brojan , and Pedro M. Reis
Advanced Materials 2014, 26, 6608–66
Curvature-induced symmetry breaking determines elastic surface patterns
Norbert Stoop, Romain Lagrange, Denis Terwagne, Pedro M. Reis, and Jörn Dunkel
Nature Materials, vol. 14, Mars 2015



