Comment les fibres textiles forment-elles un fil?
Le fil de coton enroulé sur la navette d’une machine à coudre est une longue chaîne de fibres naturellement courtes. Celles-ci ne tiennent ensemble ni par des nœuds, ni par une colle mais simplement par l’enroulement des fibres les unes sur les autres qui sont ainsi fixées grâce aux forces de frottement. Et des fils de plusieurs dizaines de mètres peuvent être obtenus avec des fibres individuelles de quelques centimètres!
Les fibres sont serrées entre elles par la tension qui crée des forces normales dues à leur courbure et des forces de frottement tangentielles qui empêchent leur glissement.
Cette technique est ancienne (on a retrouvé des fils en fibres tressées dans de nombreux sites préhistoriques dont certains datant jusqu’à il y a 40 000 ans) et toujours utilisée dans les filatures. Au cours des siècles de nombreux scientifiques se sont penchés sur ce phénomène sans trouver un modèle le décrivant parfaitement.
Deux scientifiques français, l’un de l’Université de Rennes, l’autre de l’Université de Paris-Saclay, ont étudié la force de liaison des fibres en fonction de l’angle de torsion qu’on leur appliquait.
Ils ont utilisé des fibres nouées ensemble à une extrémité, comme un gland de couturière. Ils ont disposé deux de ces glands avec leurs nœuds en directions opposées en intriquant leurs extrémités libres (Fig.1.a). Ils ont alors appliqué une torsion d’un angle total θ à l’ensemble en faisant tourner les 2 nœuds (Fig.1.b).
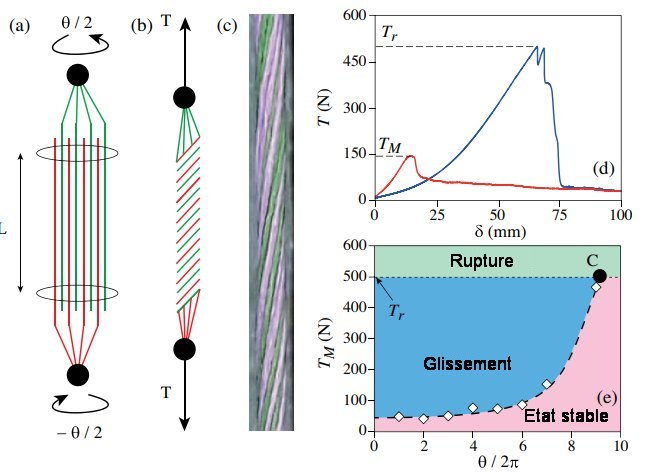
Fig.1. Préparation d’un fil modèle
a) Avant torsion.
b) Après torsion.
c) Photo d’un fil fait de fibres de coton après torsion.
d) Forces de traction en fonction du déplacement δ pour un fil de coton de longueur L= 800 mm : en bleu θ= 11×2π, en rouge θ= 3×2π
e) Force de traction maximum en fonction des angles de torsion (fil de coton, L = 800 mm). La ligne en pointillé correspond à la force de rupture.
Tiré de Twist-Controlled Force Amplification and Spinning Tension Transition in Yarn
Antoine Seguin , Jerôme Crassous
PHYSICAL REVIEW LETTERS 128, 078002 (2022) avec autorisation.
La tension nécessaire pour défaire les fils varie continûment et rapidement avec la torsion du fil obtenu.
On voit (Fig.1.d) que, si l’angle de torsion est assez faible , la force de tension appliquée augmente d’abord, atteint une valeur maximum (TM) puis diminue lentement. A cela est associé un faible glissement relatif des deux glands.
Pour des torsions élevées, au contraire, on observe une chute rapide de la force qui survient après le maximum de la force (notéTr). Cela est associé à la rupture d’un ou plusieurs brins du fil.
La figure1.e montre la variation de TM en fonction de l’angle de torsion. TM reste quasi-constante jusqu’à une torsion de θ= 5×2ϖ c’est-à-dire due à 5 tours pour ce fil, puis augmente rapidement jusqu’à une torsion de 9 tours où TM atteint Tr au point C et il y a rupture du fil.
On voit donc qu’augmenter la torsion augmente la force de liaison entre les fibres. A l ‘origine les fibres se séparent facilement, mais dès que l’on impose la torsion, il devient difficile de les séparer. Mais une trop forte torsion peut entraîner que la force de tension atteigne la limite de rupture.
Antoine Seguin et Jérôme Crassous ont fait de nombreuses expériences de ce type avec des fibres, soit de coton, soit de lin. Ils les ont interprétées avec un modèle des fils obtenus par torsion.
Celui- ci montre que la transition entre un assemblage de fibres libres et les mêmes liées par la torsion est contrôlée par un nombre sans dimension qu’ils ont nommé le nombre d’Hercule H; il ne dépend que de l’angle de torsion, du coefficient de frottement entre fibres et de facteurs géométriques : longueur et rayon du fil.
La résistance maximum d’un fil est atteinte pour H compris entre deux valeurs Hcritique et Hrupture prévisibles par le calcul. Pour le coton, on trouve que le rayon optimal est de 80 µm, ce qui correspond à la valeur couramment utilisée.
Un tel modèle se prête aux simulations de divers fils, dont on peut ainsi prédire les propriétés de façon quantitative.
Il n’est pas indispensable d’utiliser ce modèle pour déterminer les résistances optimales de fils de coton ou de cordes de chanvre. Car, pour ceux-ci, des milliers d’années de fabrication ont déjà abouti à une parfaite connaissance de celles-ci.
Mais on cherche beaucoup maintenant à réaliser des fils mixtes, mélange de coton avec du lin ou de nombreuses fibres synthétiques. Dans ces cas, la prédiction par ce modèle devient d’une grande utilité.
Pour en savoir plus :
Twist-Controlled Force Amplification and Spinning Tension Transition in Yarn
Antoine Seguin , Jerôme Crassous
PHYSICAL REVIEW LETTERS 128, 078002 (2022




