Un regard neuf sur la fonction d’onde de l’atome d’hydrogène
La fonction d’onde est un des concepts fondamentaux de la physique quantique. Dans l’interprétation dite de Copenhague et due à Bohr, elle permet d’estimer la probabilité d’obtenir un résultat de mesure sur un système quantique, par exemple une mesure de l’énergie, de la position ou de la vitesse d’une particule quantique. Bien qu’elle ait un rôle prééminent en mécanique quantique, on ne peut facilement la mesurer directement ou l’observer, car chaque mesure ne révèle qu’une partie de la fonction d’onde sous-jacente. Une équipe internationale dirigée par Aneta Stodolna, du FOM Institute for Atomic and Molecular Physics (AMOLF) à Amsterdam, Pays-Bas a pu, par une méthode de photo-ionisation, obtenir directement la structure nodale de l’orbite d’un électron d’un atome d’hydrogène placé dans un champ électrique. Cette expérience avait été proposée il y a trente ans par des physiciens théoriciens russes.
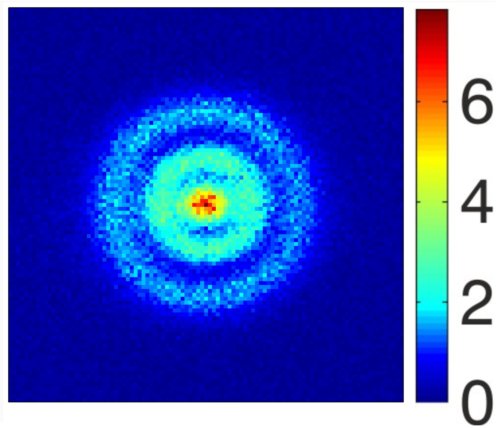
Fig.1. Une des images obtenues par photo-ionisation de la structure des orbitales sphériques des électrons d’un atome d’hydrogène excité dans un état de Rydberg. Crédit A. Stodolna, M. J. J. Vrakking,© PRL, 2013.
L’atome d’hydrogène est le plus simple de tous les atomes. Il est composé d’un proton chargé positivement et d’un électron chargé négativement. La mécanique quantique permet de résoudre complètement ce système sans approximation. Les chercheurs de AMOLF ont ainsi pu voir leurs résultats s’accorder avec la théorie quantique.
Le dispositif expérimental
Un faisceau d’atomes d’hydrogène est obtenu dans un premier compartiment à vide par photo-dissociation d’un gaz d’hydrogène sulfuré H2S sous l’effet d’un rayonnement laser de longueur d’onde λ=213 nm. Un champ électrique de 808V/cm parallèle à l’axe du faisceau est appliqué entre les plaques b et c, (fig.2). Un laser de longueur d’onde λ= 243 nm excite les atomes de l’état de base à un niveau d’énergie plus élevé. Un troisième laser accordable ( λ = 365-367 nm) les excite dans des états finaux de haute énergie appelés « états de Rydberg ». Ce laser est accordé pour exciter uniquement des états de nombre quantique principal égal à 30. La somme du champ électrique continu et de celui du rayonnement de ce laser augmente assez l’énergie des électrons de ces états pour les ioniser, c’est-à-dire les affranchir de l’interaction avec le proton et les libérer. Ils sont alors accélérés par le champ électrique et vont exciter un photo-détecteur plan muni d’un écran phosphorescent. Une caméra enregistre la position des électrons. Une lentille électrostatique placée avant le photo-détecteur multiplie par dix environ la taille des images.
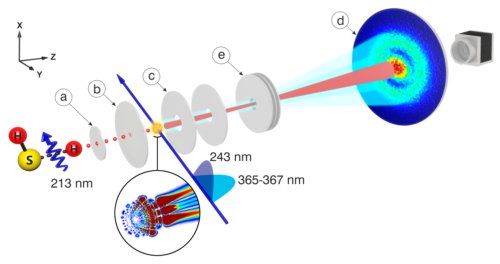
Fig.2. Schéma de l’expérience. En dissociant du gaz H2S par un faisceau laser de longueur d’onde 213 nm, on obtient un faisceau d’hydrogène atomique H qui passe à travers des diaphragmes (a, b) dans un compartiment spectroscopique b-c. Les atomes d’hydrogènes dans leur état de base sont excités par un laser à 243 nm. Puis un laser ultraviolet (365-367 nm) les excite dans un état de haute énergie appelé état de Rydberg . Le champ régnant entre les électrodes b et c ionise les atomes et accélère les électrons ainsi libérés vers un détecteur (d) plan à écran fluorescent précédé d’une lentille électrostatique (e) qui multiplie par 10 le diamètre de l’image enregistrée. Une caméra enregistre l’image de fluorescence. Crédit A. Stodolna, M. J. J. Vrakking,© PRL, 2013
Des aperçus uniques des orbitales de l’atome d’hydrogène
La prédiction théorique faite il y a trente ans par des physiciens russes était que la figure d’interférence que l’on pouvait obtenir par photo-ionisation d’électrons dans un état quantique était proportionnelle au carré du module de la fonction d’onde. L’expérience réalisée par A. Stodolna et al. a confirmé cela (Fig.3). En accordant en fréquence le laser ultraviolet, ils ont excité des états de Rydberg dont le nombre quantique principal était n= 30 mais dont le nombre quantique n1 prenait les valeurs 0, 1, 2, 3. Et ils ont obtenu des images dont le nombre d’anneaux de faible intensité, les nœuds, coïncide avec le nombre quantique n1. La structure nodale de la fonction d’onde est ainsi mise en évidence.
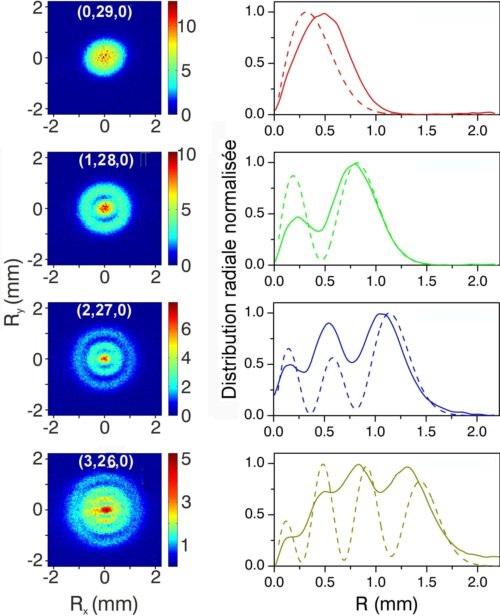
Fig.3. Observation expérimentale de la structure nodale transversale de quatre états quantiques de l’atome d’hydrogène. Les quatre images de gauche sont celles obtenues pour 4 états caractérisés par leurs nombres quantiques (n1, n2, m) indiqués sur chaque image. Ces quatre états ont le même nombre quantique principal n=30. Les anneaux d’interférence observés montrent que le nombre de franges annulaires de faible intensité (les nœuds) correspond exactement au nombre n1 de l’état quantique excité. A droite de chaque image figure l’échelle d’intensité en fausses couleurs utilisée.
Les courbes de droite représentent, en trait solide, la valeur mesurée expérimentalement de la probabilité de distribution de l’électron en fonction de la distance R au centre et, en pointillé, la valeur calculée de celle-ci. L’image d’interférences reflète directement la structure nodale de la fonction d’onde. Crédit A. Stodolna, M. J. J. Vrakking,© PRL, 2013.
Ces travaux ont abouti à la réalisation d’un véritable « microscope quantique à photo-ionisation ». On pourra l’utiliser dans de nombreuses recherches sur l’atome et les molécules. Il sera intéressant de voir comment l’atome réagit à un champ magnétique et d’étudier la dynamique de l’électron au cours du temps. L’imagerie des orbitales peut être d’une grande utilité pour l’étude des liaisons chimiques. Enfin l’équipe de AMOLF a commencé à appliquer cette technique à l’étude de l’atome d’hélium dans lequel on a 2 électrons autour du noyau.
Pour en savoir plus :
A. S. Stodolna, A. Rouzée, F. Lépine, S. Cohen, F. Robicheaux,
A. Gijsbertsen, J. H. Jungmann, C. Bordas, and M. J. J. Vrakking,
“Hydrogen Atoms under Magnification:
Direct Observation of the Nodal Structure of Stark States,”
Phys. Rev. Lett. 110, 213001 (2013).